题目描述

本题译自 eJOI2023 Problem B. Teleporters

Anna 和 Beka 位于坐标线上的不同点，计划在某个点相遇。他们唯一的移动方式是使用传送器。

共有 $N$ 个传送器，第 $i$ 个传送器位于坐标 $c_i$，运行频率为 $f_i$。然而，并非所有传送器都可用。只有频率范围在 $[L, R]$ 内的传送器可以使用。

使用一个传送器需要一分钟，并将用户传送到一个关于传送器位置的原始坐标的镜像坐标。换句话说，如果原始坐标是 $x_1$，那么使用第 $i$ 个传送器后，结果坐标 $x_2$ 将满足等式 $(x_1 + x_2)/2 = c_i$。

每分钟，Anna 和 Beka 必须使用一个可用的传送器（不一定是不同的）。他们在传送期间会进行通信，他们在这分钟的不适度是 Anna 使用的传送器频率和 Beka 使用的传送器频率的差的绝对值。旅行的整体不适度定义为他们经历过的最大不适度。

你需要回答 $Q$ 个不同的询问，对于每一个询问，你的任务是确定 Anna 和 Beka 是否能够使用可用的传送器相遇，如果可以，最小的旅行整体不适度是多少。一个询问由四个整数表示：

• $A$：Anna 的起始坐标
• $B$：Beka 的起始坐标
• $L$：可用传送器的最小频率
• $R$：可用传送器的最大频率

对于每个询问，如果他们能够相遇，则输出旅行整体不适度，否则输出 $-1$。请注意，我们并不关心总旅行时间。

输入格式

第一行包含两个整数：$N$ 和 $Q$。

第二行包含 $N$ 个整数：$c_1, c_2, \ldots , c_N$。

第三行包含 $N$ 个整数：$f_1, f_2, \ldots , f_N$。

接下来的 $Q$ 行每行有四个整数 $A, B, L, R\ (A \neq B)$，表示一个询问。

输出格式

输出一行 $Q$ 个空格分隔的整数，表示询问 $1, 2, \ldots ,Q$ 的答案。

4 3
4 6 8 10
7 1 9 4
3 11 1 50
3 11 1 5
5 7 1 1

2 3 -1

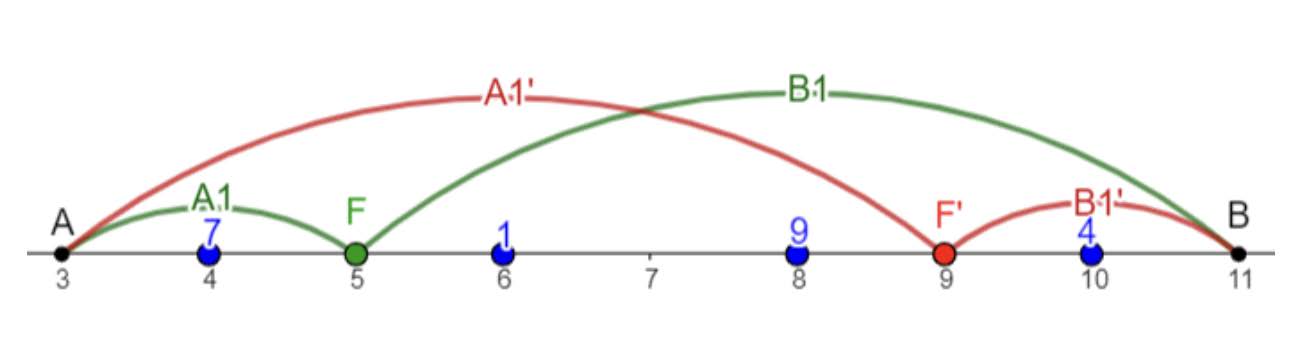
在第一个询问中，如果 Anna 使用传送器 $2$ 而 Beka 使用传送器 $4$，他们将在坐标 $9$ 相遇，不适度为 $|1 - 4| = 3$。

一个更好的方案是 Anna 使用传送器 $1$ 而 Beka 使用传送器 $3$；在这种情况下，他们在 $F = 5$ 相遇，并且经历了 $|7 - 9| = 2$ 的不适。

在第二个询问中，由于频率范围的限制，没有更好的选项。

在第三个询问中，只有一个可用的传送器，无法相遇。

3 3
-2 1 -1
10 1 3
-6 6 20 20
-6 6 0 20
-6 6 2 20

-1 2 7

坐标可以是负数。

数据范围与提示

对于所有输入数据，满足：

• $2 \leq N \leq 5\times 10^4$
• $1 \leq Q \leq 5\times 10^4$
• $1 \leq f_i \leq 10^9\ (1\leq i\leq N)$
• $-10^9 \leq c_i, A, B \leq 10^9\ (1\leq i\leq N)$
• $1 \leq L \leq R \leq 10$

详细子任务附加限制及分值如下表所示。

子任务	附加限制	分值
$1$	$N, Q \leq 10;|c_i|, f_i \leq 50\ (1\leq i\leq N)$	$11$
$2$	$N \leq 100;L = 1;R = 100;|c_i|, f_i \leq 100\ (1\leq i\leq N)$	$10$
$3$	$N = 2;L = 1;R = 10^9$	$5$
$4$	$N \leq 1000;L = 1;R = 10^9;f_i = 1\ (1\leq i\leq N)$	$9$
$5$	$L = 1;R = 10^9;f_i = 1\ (1\leq i\leq N)$	$6$
$6$	$N \leq 1000;L = 1;R = 10^9$	$7$
$7$	$L = 1;R = 10^9$	$17$
$8$	$L = 1$	$8$
$9$	$N, Q \leq 2\times 10^4$	$14$
$10$	无附加限制	$13$