题目描述

本题译自 eJOI2023 Problem E. Tree Infection

给定一个由 $N$ 个顶点组成的有根树，以及整数 $R$ 和 $M$。顶点从 $1$ 到 $N$ 编号，其中顶点 $1$ 为根。树中的其他每个顶点都有一个父节点。

如果选择一个顶点 $s$，它和它距离不超过 $R$ 的所有后代（即从 $s$ 向下沿着边可以到达的顶点）都会被感染， 其中距离是指顶点之间的边数。当且仅当 $u$ 和 $v$ 都没有被感染，且它们之间的路径上被感染的顶点数不超过 $M$ 时，顶点 $u$ 才能从顶点 $v$ 到达。

对于每个可能的选择顶点 $s$ $(1 \leq s \leq N)$，你必须计算顶点对 $(u, v)$ 的数量，满足 $1 \leq u < v \leq N$ 且 $u$ 和 $v$ 互相可达。

输入格式

第一行包含三个整数：$N$，$R$ 和 $M$。

第二行包含 $N - 1$ 个整数：$p_2, p_3, \ldots ,p_N$，分别表示顶点 $2, 3, \ldots ,N$ 的父节点。

输出格式

输出 $N$ 行，每行一个整数。第 $s$ 行表示当选择顶点为 $s$ 时的顶点对数量。

13 2 2
1 2 3 4 3 6 6 8 2 10 11 1

16
4
15
55
66
36
66
55
66
45
55
66
66

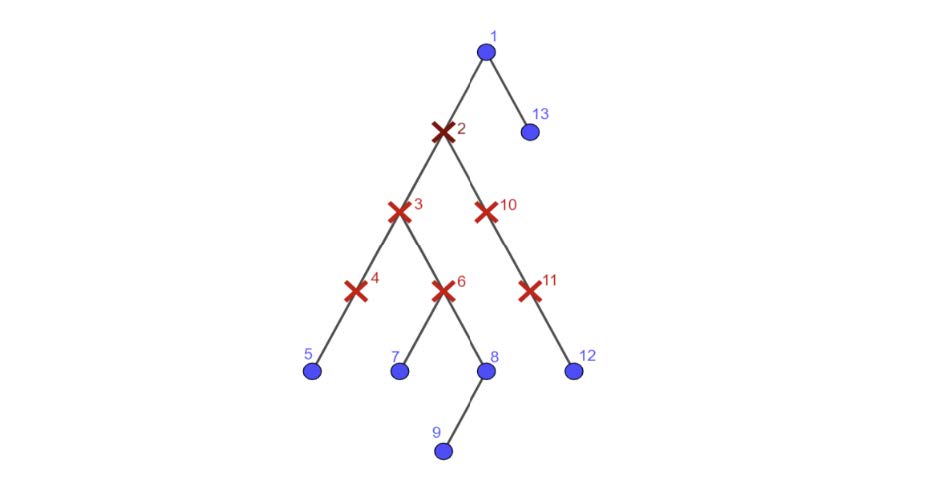
上图对应于 $s = 2$。

可达的顶点对有：$(1,13), (7,8), (7,9), (8,9)$。

这个列表不包括顶点对 $(1,2)$，因为顶点 $2$ 被感染了。同样，顶点对 $(1,5)$ 也不在列表中，因为 $1$ 和 $5$ 之间的路径上有三个被感染的顶点（$2$，$3$ 和 $4$）。

3 0 1
1 2

1
1
1

数据范围与提示

对于所有输入数据，满足：

• $2 \leq N \leq 5\times 10^5$
• $1 \leq p_i < i$ $(2 \leq i \leq N)$
• $0 \leq R \leq N - 1$
• $0 \leq M \leq 2 \times R + 1$

详细子任务附加限制及分值如下表所示。

子任务	附加限制	分值
$1$	$N \leq 300$	$20$
$2$	$R = 0$	$14$
$3$	$M = 2 \times R + 1$	$15$
$4$	$M = 2 \times R - 1$	$10$
$5$	$N \leq 5000$	$16$
$6$	无附加限制	$25$