注意事项

在 LibreOJ 上，由于语言限制，目前只支持以下语言的提交：

• C++（标准为 C++ 17 及以上）

请在提交源代码前添加 #include "sprout.h"。

题目描述

题目译自 2019년도 국제정보올림피아드 대표학생 선발고사 - 2차 선발고사 T1 「새싹」

巴库将一块大的正方形地均匀分割成了 $N \times N$ 个小方形田地。在每块田地里撒下了 $P$ 颗种子，一周后，有些种子发了芽，有些还没有发芽。比如，下面的图显示了 $6 \times 6$ 田地中每块田地发芽的情况。最左上角的田地里有两颗芽，而最右下角的田地里只有一颗芽。

观察田地时，巴库想到了最近学到的中位数。中位数是奇数个给定值中的一个，当这些值排序时，正好位于中间的那个值。比如，五个给定值是 $0,1,2,2,3$ 时，中位数是 $2$。

巴库想知道中位数和平均数之间的差异有多大，所以他决定比较每块田地发芽数量的中位数和平均数。为了进行多种情况的比较，他决定在相邻的 $K \times K$ 个田地上计算中位数和平均数。这样的话，可以在给定的 $N \times N$ 田地上总共进行 $(N-K+1) \times(N-K+1)$ 次比较。

例如，对于上图中的田地，用 $3 \times 3$ 的区域计算中位数和平均数结果如下表。最左上角的 $3 \times 3$ 田地中发芽数量是 $2, 1, 0, 0, 1, 0, 2, 0, 1$，因此中位数是 $1$，平均数是 $7 / 9$。最右上角的 $3 \times 3$ 田地中，中位数是 $0$，平均数是 $8 / 9$。

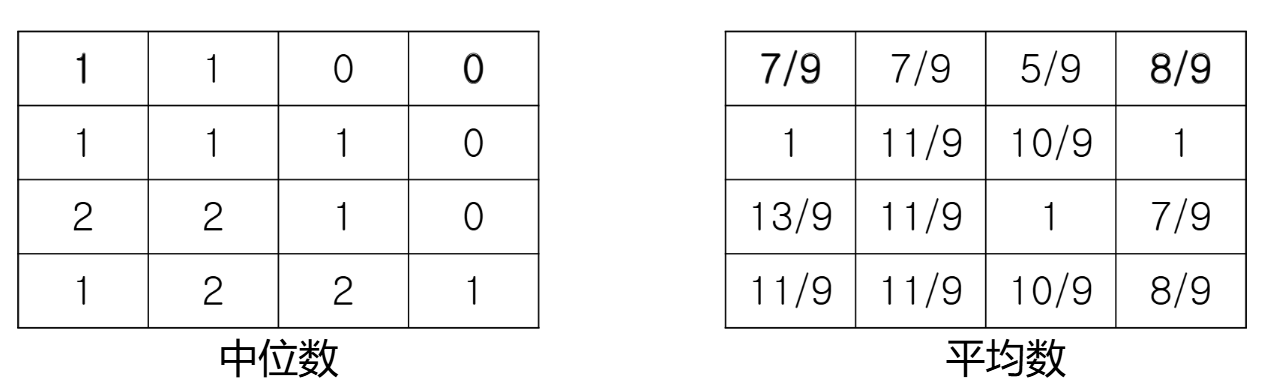
巴库想知道中位数和平均数差值的最大值。在上例中，最大差值出现在下图中标红色边框的部分，中位数是 $0$，平均数是 $1$，两者差值是 $1$。

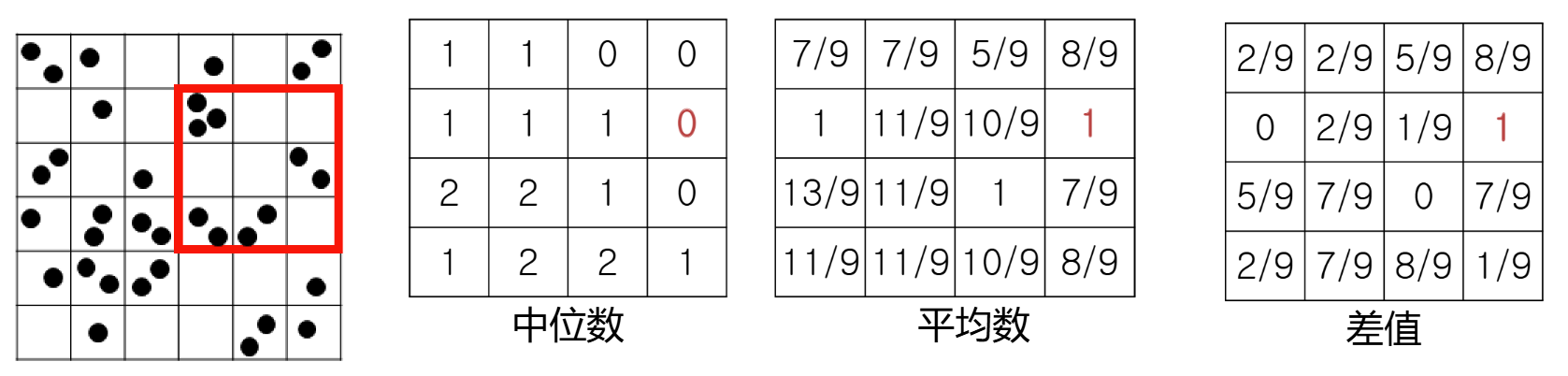
巴库为了方便计算，决定找出中位数和平均数差值乘以 $K^{2}$ 后的最大值。所以，在上例中最大值是9。你需要为巴库实现以下函数：

int diff(int K, int V[][]);

该函数只会被调用一次，V 是大小为 $N \times N$ 的数组（向量），每块田地发芽的数量 V[0..N-1][0..N-1] 是传入的参数。函数需要计算出 $K \times K$ 区域中中位数和平均数的差值乘以 $K^{2}$ 的最大值并返回。

实现细节

你需要提交一个名为 sprout.cpp 的文件。该文件必须实现以下函数：

int diff(int K, int V[][]);

这些函数必须按照上述描述工作。当然，你可以创建和使用其他函数，但不得进行任何输入输出操作或访问其他文件。

示例评测程序

示例评测程序按以下格式读取输入：

• 第 $1$ 行：$N K$，其中 $N$ 表示田地的大小，$K$ 表示区域的大小
• 接下来的 $N$ 行：$V_{i,0}\, V_{i,1}\,\cdots \,V_{i,N-1}$，其中 $(V_{i,0}\, V_{i,1}\, \cdots\, V_{i,N-1}$ 表示第 $i$ 行的发芽数量

示例评测程序会输出你在 diff() 函数中返回的值。

6 3
2 1 0 1 0 2
0 1 0 3 0 0
2 0 1 0 0 2
1 2 2 2 2 0
1 2 2 0 0 1
0 1 0 0 2 1

9

4 3
10 20 10 20
20 10 20 10
10 20 10 20
20 10 20 10

40

数据范围与提示

对于所有输入数据，满足：

• $1 \leq N \leq 2\,000$
• $K$ 为奇数，$1 \leq K \leq N$
• $0 \leq V_{i,j} \leq 30$ $(0 \leq i, j \leq N-1)$

详细子任务附加限制及分值如下表所示。

子任务	分值	附加限制
$1$	$17$	$N \leq 100$
$2$	$24$	$N \leq 300$
$3$	$42$	$N \leq 700$
$4$	$67$	无附加限制