题目描述

题目译自 eJOI2024 Day2 T2. Sweets

桑杜高中毕业后决定追求他作为糖果销售员的梦想。摩尔多瓦的城市巴尔蒂有 $N$ 个市场，市场之间有街道连接。市场的结构非常有趣。通过一些街道可以从一个市场到达任何其他市场，并且市场之间恰好有 $N-1$ 条街道。而且，桑杜目前居住在市场 $1$。换句话说，这些市场形成了一棵以市场 $1$ 为根的树结构。

此外，每个市场 $i$ 有一个坚韧度 $t_{i}$ 和学习等级 $l_{i}$。最初每个市场的学习等级为 $0$，而桑杜的销售技能等级也为 $0$。

当桑杜访问市场 $i$ 时，他的销售技能等级增加 $l_{i}$。如果他的销售技能等级至少为 $t_{i}$，那么桑杜在市场 $i$ 就会成功。注意，不论桑杜是否在市场 $i$ 成功，他的销售技能等级都会在他进入市场 $i$ 时增加。这意味着他的销售技能等级在他尝试做任何事情之前就增加了。

而且，由于巴尔蒂是一个非常繁忙的城市，在接下来的 $Q$ 天中每天都会发生一个事件。在第 $j$ 天，事件 $j$ 将发生。事件由两个正整数 $u_{j}$ 和 $x_{j}$ 描述，表示在第 $j$ 天，市场 $u_{j}$ 将发生事件，对应市场的学习等级将永久增加 $x_{j}$。换句话说，事件 $j$ 意味着 $l_{u_{j}}=l_{u_{j}}+x_{j}$。

桑杜计划访问一些市场并在其中出售糖果。他会选择一个市场 $k$，从市场 $1$ 开始依次访问到市场 $k$ 路径上的所有市场。桑杜希望在尽可能多的市场中取得成功。无论他是否成功，他都会继续向市场 $k$ 前进。此外，每天桑杜都从市场 $1$ 开始，他的销售技能等级重置，每天开始时他的销售技能等级为 $0$。

对于第 $j$ 天，帮助桑杜求出在选择最优的 $k$ 的情况下，他在多少个市场获得成功。

输入格式

输入的第一行包含两个整数 $N$ 和 $Q$ $(1 \leq N, Q \leq 5 \cdot 10^{5})$。

第二行包含 $N-1$ 个整数 $p_{2}, \ldots, p_{N}$ $(1 \leq p_{i} < i)$，表示存在一条边连接 $p_{i}$ 和 $i$，且 $p_{i}$ 是 $i$ 的父节点。

第三行包含 $N$ 个整数 $t_{1}, t_{2}, \ldots, t_{N}$ $(0 \leq t_{i} \leq 10^{9})$，表示给定市场的坚韧度。

接下来 $Q$ 行，表示在第 $j=1,2,\ldots, Q$ 天发生的事件。

第 $j$ 行包含两个整数 $u_{j}, x_{j}$ $(1 \leq u_{j} \leq N, 1 \leq x_{j} \leq 10^{9})$，描述第 $j$ 天的事件。

输出格式

输出 $Q$ 行，在第 $j$ 行输出第 $j$ 天的答案。

12 5
1 1 3 3 1 6 7 1 9 10 11
1 2 6 3 5 4 6 5 2 3 4 5
1 1
1 1
3 2
6 3
9 6

1
2
2
3
5

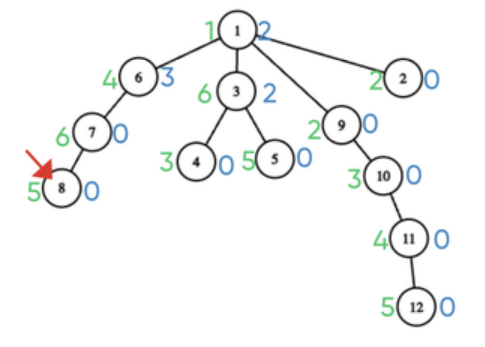
第一个样例的初始树如下图所示。在图像中，市场右侧的数字表示该市场的学习等级，市场左侧的数字表示对应市场的坚韧度。

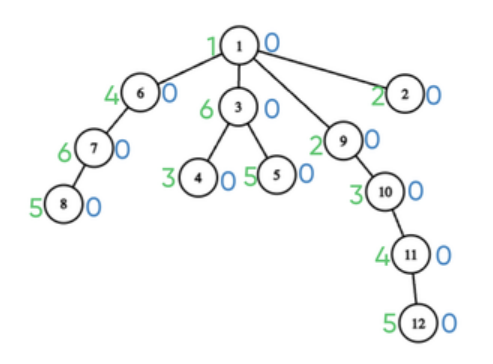
在第一天之后，树的变化如下图所示，桑杜可能去的一个最佳市场是 $6$，因为市场 $1$ 的学习等级至少等于其坚韧度，而坚韧度也为 $1$，因此最大答案为 $1$。

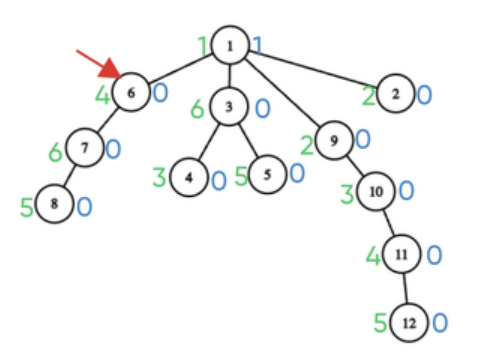
在第二个事件后，答案变为 $2$，因为桑杜可以选择去市场 $2$，从市场 $1$ 获得 $2$ 的销售技能等级，这大于等于市场 $1,2$ 的坚韧度。

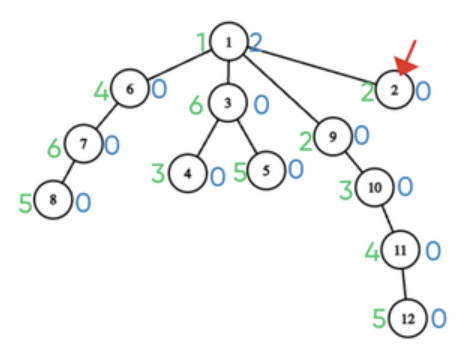
在第三个事件后，答案没有变化，但树的变化如下所示：

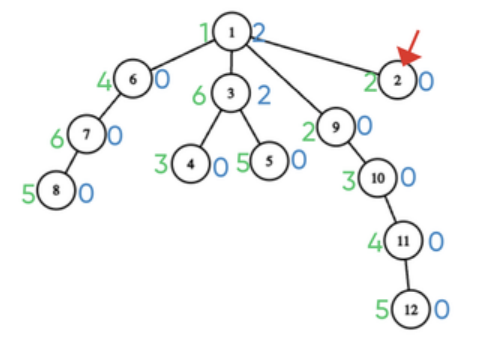
在第四个事件后，答案变为 $3$，因为如果桑杜从市场 $1$ 开始，他的销售技能等级将提高到 $2$，这意味着他在市场 $1$ 成功。然后，他前往市场 $6$，他的销售技能等级提高到 $5$，这意味着他在市场 $6$ 也成功了。然后，他前往市场 $7$，没有成功，接着他前往市场 $8$，成功了，因为 $5 \geq 5$。

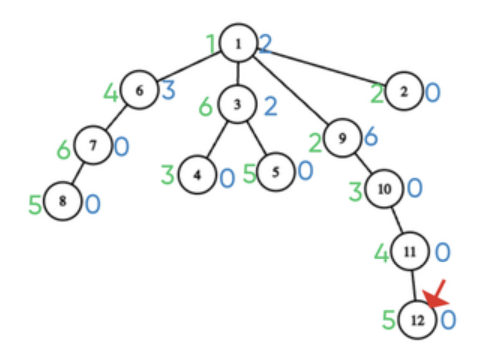
对于最后一个事件，树的变化如下所示，最佳答案为 $5$，因为桑杜可以去市场 $12$，并在市场 $1,9,10,11,12$ 取得成功。

5 4
1 2 3 4
1 2 5 6 7
1 1
1 2
1 1
1 2

1
2
2
4

5 5
1 1 1 1
1 2 3 4 5
4 4
2 2
5 5
1 1
3 3

1
1
1
2
2

数据范围与提示

对于所有输入数据，满足：

• $1 \leq N, Q \leq 5 \cdot 10^{5}$
• $1 \leq p_{i} < i$
• 对于所有 $i$ $(1 \leq i \leq N)$，$0 \leq t_{i} \leq 10^{9}$
• 对于所有 $j$ $(1 \leq j \leq Q)$，$1 \leq u_{j} \leq N$
• 对于所有 $j$ $(1 \leq j \leq Q)$，$1 \leq x_{j} \leq 10^{9}$

详细子任务附加限制及分值如下表所示。

子任务	分值	附加限制
$1$	$7$	$p_{i}=1$ $(1 < i \leq N)$，$N, Q \leq 2000$
$2$	$8$	$N, Q \leq 2000$，$p_{i}=i-1$ $(1<i \leq N)$
$3$	$17$	$p_{i}=i-1$ $(1<i \leq N)$
$4$	$12$	$N, Q \leq 2000$
$5$	$21$	$u_{j}=1$
$6$	$24$	$N, Q \leq 10^{5}$
$7$	$11$	无附加限制