题目描述

译自 ROI Regional 2025 Day2 T4. Туристический маршрут

一群小学生来到一座新城市游览，决定参观这里的名胜古迹。我们可以将这座城市看作一个 $n \times m$ 的矩形网格，其中某些格子上有景点。

小伙伴们从格子 $(1, 1)$ 开始他们的旅程，想要到达格子 $(n, m)$，然后再返回起点。此外，城市中有 $k$ 个景点，位于格子 $(x_1, y_1), \ldots, (x_k, y_k)$，他们一定要全部参观到。

他们可以花费一分钟从格子 $(a, b)$ 移动到与之相邻的格子 $(c, d)$，如果它们在边上相邻，即满足 $|a - c| + |b - d| = 1$。显然，完成整个路线至少需要 $2n + 2m - 4$ 分钟，我们只考虑这种时长的路线。

我们称一条路线为 有趣的路线，如果满足以下条件：

• 他们花费恰好 $2n + 2m - 4$ 分钟完成这条路线；
• 路线中的每个格子最多经过一次；
• 路线必须经过所有包含景点的格子。

请帮助小学生们计算一共有多少条不同的有趣路线。由于结果可能非常大，请输出对 $10^9 + 7$ 取模的结果。

输入格式

第一行输入三个整数 $n$、$m$ 和 $k$ $(3 \leq n, m \leq 10^6, 0 \leq k \leq 2000)$。

接下来的 $k$ 行中，每行包含两个整数 $x_i, y_i$ $(1 \leq x_i \leq n, 1 \leq y_i \leq m)$，表示第 $i$ 个景点的位置。保证所有的 $(x_i, y_i)$ 都是不同的。也就是说，对于任意不同的索引 $i$ 和 $j$ $(1 \leq i < j \leq n)$，有 $x_i \neq x_j$ 或 $y_i \neq y_j$。

输出格式

输出一个整数，表示有趣路线的数量对 $10^9 + 7$ 取模的结果。

3 4 2
2 2
2 3

6

以下展示了第一个样例中所有的有趣路线，包含景点的格子用星号表示。：

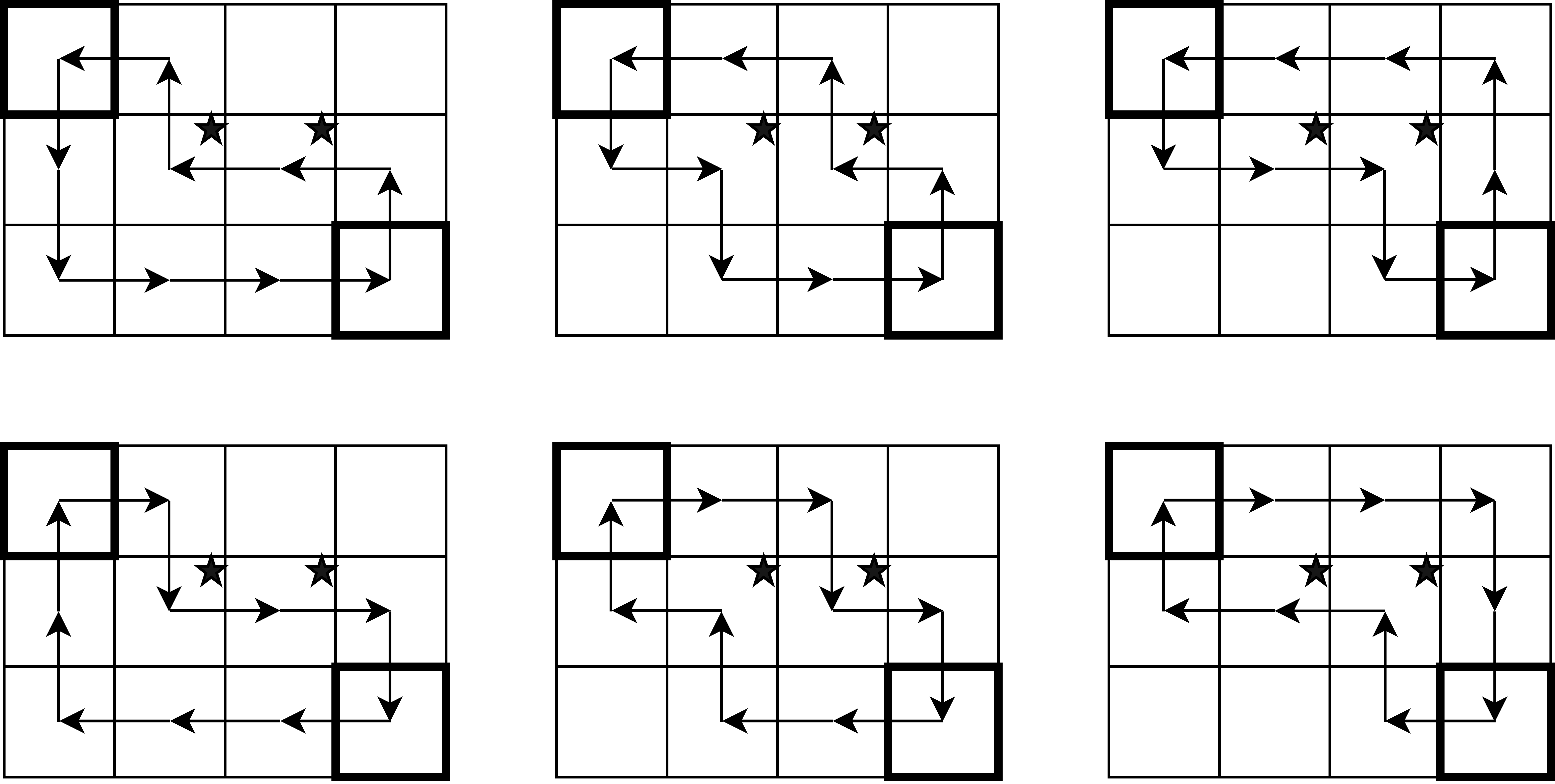
3 4 3
3 1
2 3
1 4

0

数据范围与提示

详细子任务附加限制及分值如下表所示。

子任务	分值	附加限制	子任务依赖
$1$	$5$	$n=3$；$m, k \leq 100$
$2$	$9$	$n, m, k \leq 5$
$3$	$6$	$n, m, k \leq 8$	$2$
$4$	$17$	$n, m, k \leq 30$	$2, 3$
$5$	$16$	$n, m, k \leq 100$	$1\sim 4$
$6$	$8$	$k=0$
$7$	$11$	$k=1$
$8$	$12$	$k \leq 16$	$2, 3, 6, 7$
$9$	$9$	$k \leq 100$	$1\sim 8$
$10$	$7$	无附加限制	$1\sim 9$