注意事项

在 LibreOJ 上，由于语言限制，目前只支持以下语言的提交：

• C++（标准为 C++ 17 及以上）

请在提交源代码前添加 #include "numbering.h"。

题目描述

题目译自 2025년도 국제정보올림피아드 대표학생 선발고사 - 2차 선발고사 T3 「넘버링」

KOI 城市由 $N$ 个交叉口和 $M$ 条双向道路组成，你可以通过这些道路在任意两个不同交叉口之间自由往来。值得注意的是，连接同一对交叉口的双向道路可能不止一条。

每个交叉口被分配了一个从 $0$ 到 $N-1$ 的独一无二的编号，每条道路也被分配了一个从 $0$ 到 $M-1$ 的独特编号。

如果一个长度为 $N$ 的整数数组 $a[0], a[1], \cdots, a[N-1]$ 满足以下条件，我们就称它为好编号：

• 对于任何一条不重复经过同一道路的路径，按访问顺序列出交叉口的编号为 $u_{0}, u_{1}, \ldots, u_{l-1}$，对应的数组值要么满足 $a[u_{0}] \leq a[u_{1}] \leq \ldots \leq a[u_{l-1}]$（单调递增），要么满足 $a[u_{0}] \geq a[u_{1}] \geq \ldots \geq a[u_{l-1}]$（单调递减）。注意，路径上可以多次经过同一个交叉口。

一个长度为 $N$ 的整数数组 $a[0], a[1], \cdots, a[N-1]$ 的多样性定义为满足 $a[u] \neq a[v]$ 且 $0 \leq u < v \leq N-1$ 的 $(u, v)$ 对的数量。

现在，给你 KOI 城市的道路网络结构，你需要编写程序，找出所有好编号中多样性的最大值。

实现细节

你需要实现以下函数：

long long max_diversity(int N, int M, vector<int> U, vector<int> V)

• N：交叉口的数量。
• M：道路的数量。
• U, V：对于所有 $0 \leq i \leq M-1$，第 $i$ 条道路连接 $U[i]$ 号交叉口和 $V[i]$ 号交叉口，且 $U[i] \neq V[i]$。
• 函数需返回所有好编号中多样性的最大值。

你提交的代码中不得包含任何输入输出函数。

样例

假设 $N = 5$，$M = 5$，$U = [0, 0, 1, 1, 2]$，$V = [1, 2, 2, 3, 4]$。

评测程序调用：

max_diversity(5, 5, [0, 0, 1, 1, 2], [1, 2, 2, 3, 4])

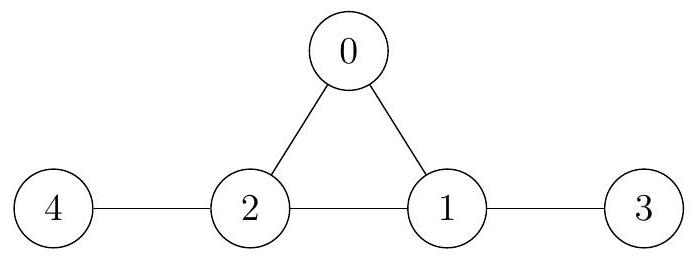
• $a = [2, 1, 1, 3, 1]$ 不是好编号。例如路径 $0 \to 1 \to 3$，对应 $a[0] = 2, a[1] = 1, a[3] = 3$，既非递增（$2 > 1 < 3$）也非递减。
• $a = [1, 1, 1, 1, 1]$ 是好编号，多样性为 $0$（无不同值对）。
• $a = [2, 2, 2, 3, 0]$ 是好编号，多样性为 $7$（不同值对有 $(0, 3), (1, 3), (2, 3), (3, 4), (0, 1), (0, 2), (1, 2)$）。

通过分析，所有好编号的多样性最大值为 $7$，因此函数应返回 $7$。

数据范围与提示

对于所有输入数据，满足：

• $2 \leq N \leq 1000000$
• $1 \leq M \leq 2000000$
• 对于所有 $0 \leq i \leq M-1$，$U[i] \neq V[i]$。
• 对于所有 $0 \leq i \leq M-1$，$0 \leq U[i], V[i] \leq N-1$。

详细子任务附加限制及分值如下表所示。

子任务	分值	附加限制
$1$	$1$	$M = N - 1$；不存在与 $4$ 条或更多道路相邻的交叉口；$N \leq 500$
$2$	$4$	$M = N - 1$；不存在与 $4$ 条或更多道路相邻的交叉口；$N \leq 5000$
$3$	$5$	$M = N - 1$；不存在与 $4$ 条或更多道路相邻的交叉口
$4$	$3$	$M = N - 1$；$N \leq 500$
$5$	$5$	$M = N - 1$；$N \leq 5000$
$6$	$28$	$M = N - 1$
$7$	$6$	$N \leq 500$；$M \leq 1000$
$8$	$10$	$N \leq 5000$；$M \leq 10000$
$9$	$38$	无附加限制

示例评测程序

示例评测程序接收以下格式的输入：

• 第 $1$ 行：$N\ M$
• 第 $2+i$ $(0 \leq i \leq M-1)$ 行：$U[i]\ V[i]$

输出格式如下：

• 第 $1$ 行：max_diversity 的返回值

请注意，示例评测程序可能与实际评测程序有所不同。