题目背景

SHOI2012 D1T3

题目描述

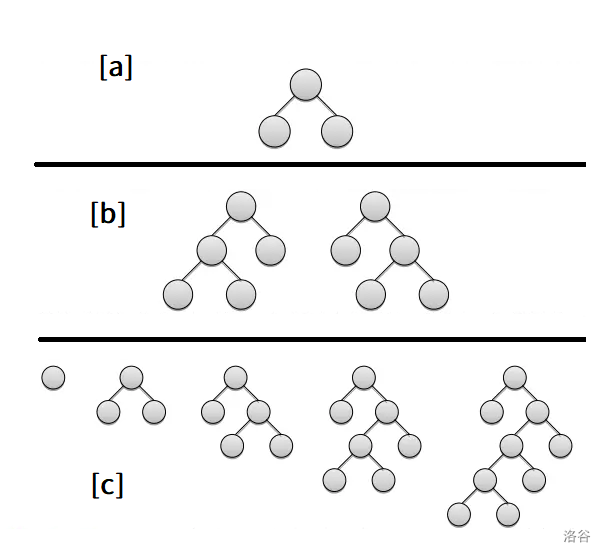
一棵含 $n$ 个叶结点的二叉树可以通过如下方式生成。初始时只有根结点。首先，将根结点展开（本题中的“展开”是指给一个叶结点添上左、右两个子结点）：

[a]

然后，等概率地随机将两个叶结点中的一个展开，即生成以下两棵树之一：

[b]

之后，每次在当前二叉树的所有叶结点中，等概率地随机选择一个，将其展开。

不断地重复这一操作，直至产生 $n$ 个叶结点为止。例如，某棵含 5 个叶结点的二叉树可能按如下步骤生成。

[c]

对于按该方式随机生成的一棵含 $n$ 个叶结点的二叉树，求：

1. 叶结点平均深度 的数学期望值。
2. 树深度 的数学期望值。约定根结点的深度为 0。

输入格式

输入仅有一行，包含两个正整数 $q$, $n$，分别表示问题编号以及叶结点的个数。

输出格式

输出仅有一行，包含一个实数 $d$，四舍五入精确到小数点后 $6$ 位。如果 $q = 1$，则 $d$ 表示叶结点平均深度的数学期望值；如果 $q = 2$，则 $d$ 表示树深度的数学期望值。

1 4

2.166667

2 4

2.666667

1 12

4.206421

2 12

5.916614

提示

【样例1、样例2说明】

数学期望值是随机变量的值乘以其概率的总和：记随机变量 $X$ 可能的取值为 $x_1,x_2,\cdots,x_n$，它们取到的概率分别为 $p_1,p_2,\cdots,p_n$，那么随机变量 $X$ 的数学期望值就是

$E(X)=\sum_{i = 1}^{n}p_ix_i$

例如，掷一枚写有 1、2、3、4、5、6 这 6 个数的均匀骰子，掷到的数的数学期望值是：

$E=\frac{1}{6}\times1+\frac{1}{6}\times2+\frac{1}{6}\times3+\frac{1}{6}\times4+\frac{1}{6}\times5+\frac{1}{6}\times6 = 3.5$

尽管 3.5 不是骰子上的某个数。又如，一道 4 选 1 的选择题，答对得 5 分，不答不得分，答错倒扣 1 分。那么，当我们不答时，一定得 0 分；而等概率地随便猜一个时，得分的数学期望值是：

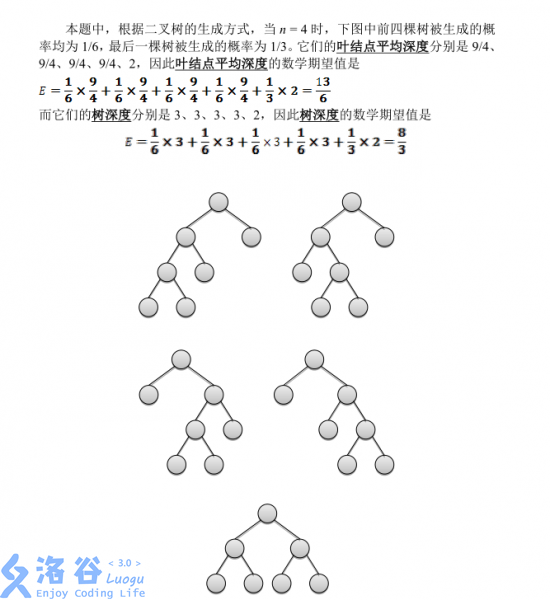
本题中，根据二叉树的生成方式，当 $n = 4$ 时，下图中前四棵树被生成的概率均为 $1/6$，最后一棵树被生成的概率为 $1/3$。它们的叶结点平均深度分别是 $9/4$、$9/4$、$9/4$、2，因此叶结点平均深度的数学期望值是

$E=\frac{1}{6}\times\frac{9}{4}+\frac{1}{6}\times\frac{9}{4}+\frac{1}{6}\times\frac{9}{4}+\frac{1}{6}\times\frac{9}{4}+\frac{1}{3}\times2=\frac{13}{6}$

而它们的树深度分别是 3、3、3、3、2，因此树深度的数学期望值是

$E=\frac{1}{6}\times3+\frac{1}{6}\times3+\frac{1}{6}\times3+\frac{1}{6}\times3+\frac{1}{3}\times2=\frac{8}{3}$

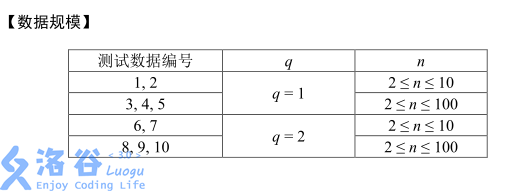
【数据规模】

测试数据编号	$q$	$n$
1,2	$q = 1$	$2\leq n\leq10$
3,4,5		$2\leq n\leq100$
6,7	$q = 2$	$2\leq n\leq10$
8,9,10		$2\leq n\leq100$